技术创新

    高墩大跨桥梁的稳定性，关系到桥梁建成后的使用和安全。本文以湖北恩施至重庆黔江高速公路工程中某高墩特大桥为例，通过建立计算模型进行计算，对该桥桥墩的稳定性进行研究，对影响桥墩稳定性的各因素进行分析，通过研究与分析，采取有效措施，保证桥梁的稳定性。为今后高墩大跨刚构桥稳定性设计提供借鉴。
1· 工程概况
湖北恩施至重庆黔江高速公路工程的某高墩特大桥，位于山区，纵横向地形差异较大，故造成设计中左右线桥的桥跨布置有所不同，左线桥分为5 联，其布孔为3 × 40 m + 4 × 40 m + 3 × 40 m + ( 65 m + 3× 120 m + 65 m) + 4 × 40 m + 4 × 40 m; 右线桥分为4 联，其布孔为4 × 40 m + 4 × 40 m + ( 65 m + 3 × 120m + 65 m) + 5 × 40 m。其中65 m + 3 × 120 m + 65 m为预应力混凝土连续刚构主桥，其余40 m 跨为先简支后连续T 梁型式。主桥上部结构为5 跨预应力混凝土连续刚构箱梁，下部结构主墩墩身采用双肢变截面矩形空心墩，基础采用桩径2． 5 m 的钻孔灌注桩基础。地质钻孔揭示，主桥桥墩处土层自上而下依次为黏土、圆砾土、粉质黏土、灰岩。
2 ·计算模型
此高速公路工程某高墩特大桥属于双薄壁高墩结构，最高墩高达99 m，桥墩的稳定性成为检算其结构稳定和安全的一个重要方面。稳定性分析通常指结构在外力作用下，平衡状态丧失，稍有扰动，结构变形急剧增大，最后使结构破坏，转化为数学表达式为求解特征值问题。结构表达式为:
| K + λKσ | = 0 ( 1)
式中: K———单元弹性刚度矩阵;
Kσ———初始应力刚度矩阵;
λ ———特征值。作用荷载为单位荷载时，特征值为屈曲荷载; 作用荷载为实际荷载时，特征值为结构安全屈曲系数( 一般大于5) 。
基于稳定性计算理论，通过MIDAS 空间分析软件，建立空间单元模型，对该桥的最不利状态———最大悬臂状态进行稳定性分析，其结构模型如图1 所示。

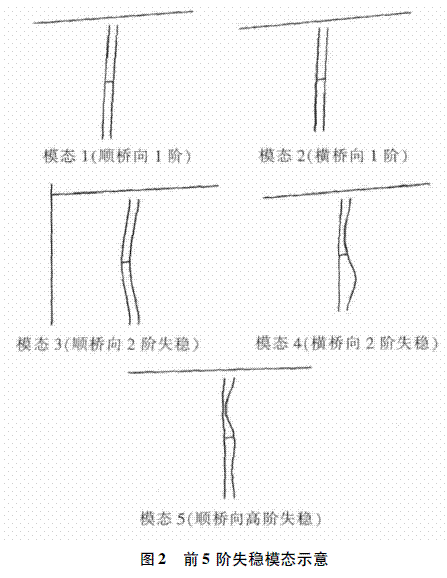
为进一步探明边界条件改变时，各因素对桥墩稳定性的影响，现利用MIDAS 空间计算软件，计算前5 阶失稳模态( 图2) 和对应的安全屈曲系数，并分析各边界因素与桥墩稳定性的关系。

3· 材料与桥墩稳定性关系分析
一般情况下，桥墩材料选用C30 或C40 混凝土，但为探明采用材料的规律，选择从C25 到C55的混凝土强度等级，并结合实际工程，在外界边界条件不变的情况下，利用MIDAS 空间计算软件，计算5 种模态下的安全屈曲系数，如表1 所示，绘制成图如图3 所示。

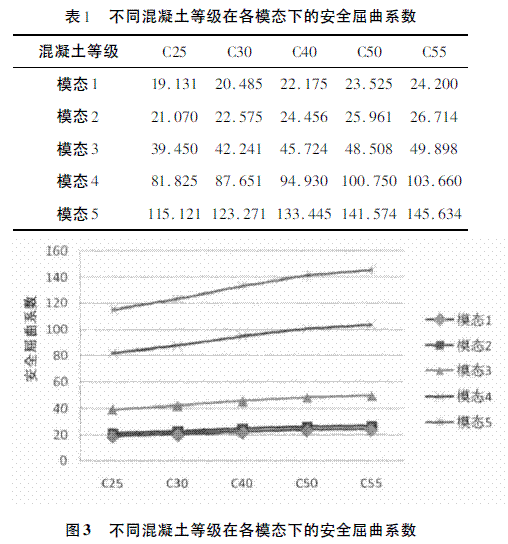
由以上计算数据可以看出，随着混凝土强度等级的提高，结构安全屈曲系数在逐渐增加，增加速度较慢。这说明混凝土强度等级的提高对桥墩安全屈曲系数有一定的积极作用。但到了某一等级时，其作用不再明显。综合计算结果、结构的安全性和经济性、施工工艺的难易程度，该桥选用C40 混凝土，安全屈曲系数最小值大于20，能满足结构稳定性和安全强度等级的要求。
4· 桥墩高度变化与桥墩稳定性关系
为探明桥墩高度变化与安全屈曲系数的规律，取墩高从60 m 到100 m，在其他外界条件不变的情况下，利用MIDAS 空间计算软件，计算5 种模态下墩高变化对应的安全屈曲系数，如表2 所示，绘制成图如图4 所示。

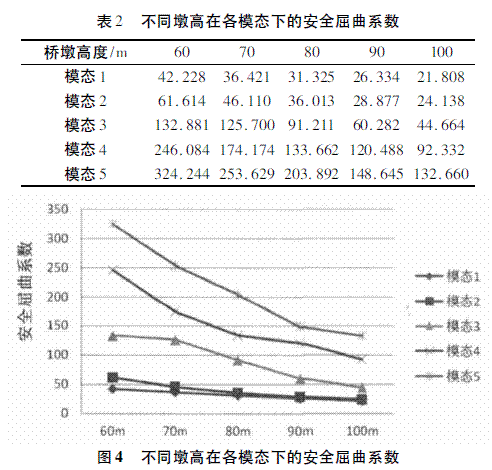
由表2 和图4 可以看出，随着墩高的改变，桥墩的稳定性与墩高成反比，墩高从60 m 增加到100m，墩高增加了66． 67%，稳定性系数降低了48． 39%，这说明桥墩越高，桥的稳定性越差。该桥设计最高墩99 m，最低墩85 m，根据稳定性计算结果，安全屈曲系数最小值大于20，桥梁的稳定性满足安全运营的要求。
5· 增加横向支撑对稳定性的影响
在桥梁工程设计中，当所需的桥墩高度较高时，经理论计算安全屈曲系数满足稳定性要求的条件下，可在双薄壁高墩之间增加一定数量的横向支撑，进一步增强桥梁的稳定性。现以桥墩高99 m，采用C40 混凝土，探讨增加横向支撑与桥墩稳定安全屈曲系数间的关系。经计算5 种模态下不同横向支撑数对应的安全屈曲系数，如表3 所示，绘制成图如图5 所示。


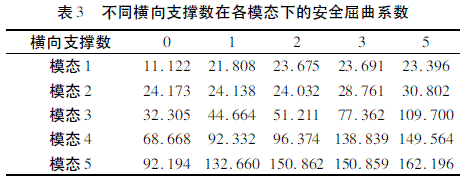
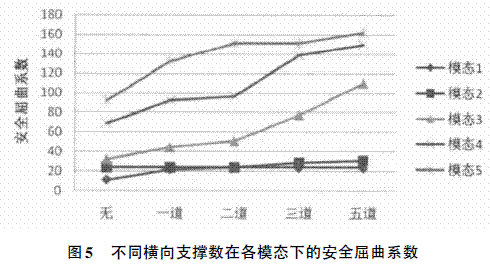
由表3 和图5 可以看出，增加1 道横向支撑时，顺桥向1 阶( 模态1) 桥墩稳定性增加比较明显，约提高1 倍，但随着横向支撑增加到5 道，顺桥向1 阶( 模态1) 安全屈曲系数变化不大。
横桥向1 阶( 模态2) 横向支撑从1 道增加到5道，安全屈曲系数增加不明显。顺桥向2 阶( 模态3) 、横桥向2 阶( 模态4) 、顺桥向高阶( 模态5) ，最小安全屈曲系数在30 以上，增加不增加横向支撑意义不大。